Model Predictive Controller Design for Heavy-duty Trucks Based on Random Forest Residual Learning
-
摘要: 近年来, 模型预测控制(MPC)在自动驾驶领域大量应用, 但依然面临车辆动力学非线性建模、实时滚动优化等困难. 基于数据驱动建立车辆动力学模型的MPC通过收集系统的输入输出数据, 直接学习动力学模型, 但依然需要额外处理环节解决实时滚动优化问题. 为此, 提出一种基于随机森林学习车辆动力学模型的方法. 先将车辆动力学模型分解为标称模型和残差模型, 然后利用两层随机森林学习残差模型. 上层用于切换不同线性模型, 下层拟合叶子节点的线性模型. 由于标称模型和残差模型均为线性模型, 滚动优化可直接使用二次规划求解器实时求解. 同时, 基于随机森林的残差模型使用多帧历史状态作为特征输入, 学习得到的残差模型保留动力学系统动态响应的延迟特性, 因此可有效消解延迟影响. 仿真测试和实车实验结果表明, 提出的MPC的跟踪精度和实时性均优于标称MPC和基于高斯过程的MPC, 并对车辆执行机构延迟具有优良的适应性.Abstract: In recent years, model predictive control (MPC) has been widely applied in autonomous driving, yet still faces challenges in nonlinear vehicle dynamics modeling and real-time rolling optimization. Data-driven MPC, which establish vehicle dynamics models by collecting the input-output data of the system to directly learn the dynamics model, still require an additional processing step to address the real-time rolling optimization problem. To tackle this issue, a method for learning the vehicle dynamics model based on random forest is proposed. The vehicle dynamics model is decomposed into a nominal model and a residual model, with a two-layer random forest learning the residual model. The upper layer is used to switch between different linear models while the lower layer fits linear models at leaf nodes. Since both nominal and residual models are linear models, the rolling optimization can be solved in real time using quadratic programming solvers. Meanwhile, the residual model based on random forest uses multi-frame historical states as feature inputs, and the learned residual model retains the delay characteristics of the dynamic response of the dynamics system, thus effectively mitigating the impact of delays. Simulation test and real-world vehicle experimental results demonstrate that the proposed MPC achieves superior tracking accuracy and real-time performance compared to nominal MPC and Gaussian process-based MPC, and exhibits excellent adaptability to vehicle actuator delays.
-
Key words:
- Model predictive control /
- residual learning /
- random forest /
- trajectory tracking /
- delay
1)1 1[8]的复现代码https://github.com/lucasrm25/Gaussian-Process-based-Model-Predictive-Control -
图 1 基于随机森林线性学习的模型预测控制系统框图
Fig. 1 Block diagram of model predictive control system based on random forest linear learning
图 2 半拖挂卡车单轨模型和误差示意图
Fig. 2 Schematic diagram of single-track model and error for semi-trailer truck
图 4 乘用车误差状态模型示意图
Fig. 4 Schematic diagram of passenger vehicle model with error states
图 12 不同延迟模型MPC跟踪横向误差
Fig. 12 Lateral tracking errors of MPC with different delay models
表 1 半拖挂卡车模型参数表
Table 1 Model parameter table of semi-trailer trucks
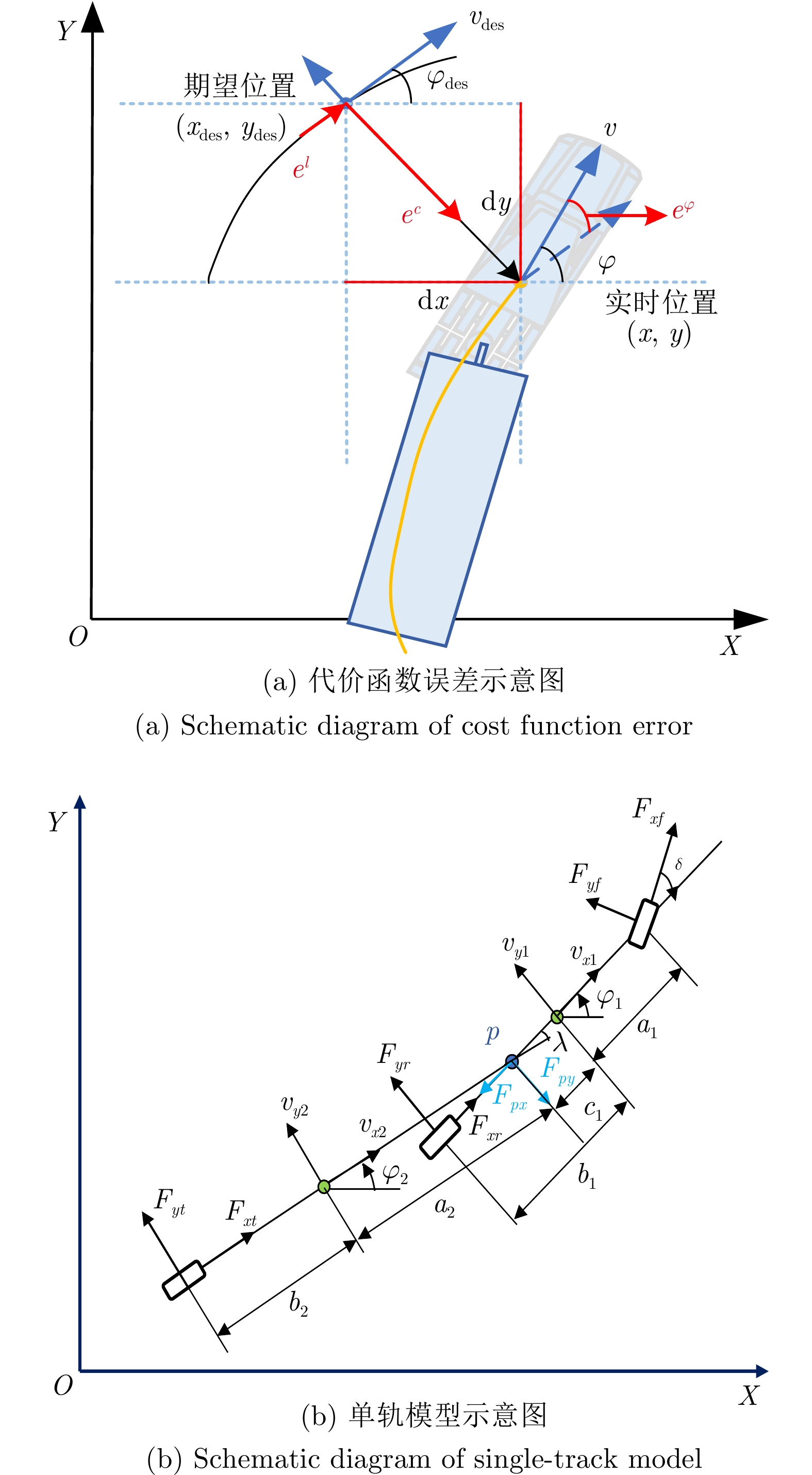
模型参数 含义 仿真数值 实车数值 $ m_1 $、$ m_2 $ (kg) 牵引车、挂车质量 7180 、10000 6870 、8000 $ I_{z1} $、$ I_{z2} $ (N$ \cdot $m$ ^2 $) 牵引车、挂车转动惯量 21863 、141676 24800 、113341 $ a_1 $、$ b_1 $、$ c_1 $ (m) 牵引车质心到前轮、后轮和铰接点的距离 1.675、1.815、0.6 1.8、2.0、0.6 $ a_2 $、$ b_2 $ (m) 挂车质心到铰接点和后轮的距离 4.426、3.102 4.426、3.102 
下载: 导出CSV
表 2 不同学习模型的计算复杂度对比表
Table 2 Computational complexity comparison table of different learning models
项目 GP Sparse GP RT RF 训练时间 $ {\rm{O}}(n^3) $ $ {\rm{O}}(s^2n) $ $ {\rm{O}}(nFD) $ $ {\rm{O}}(T\times \tau\log_{}{\tau}) $ 训练空间 $ {\rm{O}}(n^2) $ $ {\rm{O}}(sn) $ $ - $ $ - $ 均值预测 $ {\rm{O}}(n) $ $ {\rm{O}}(s) $ $ {\rm{O}}(FD) $ $ {\rm{O}}(T\times FD) $ 方差预测 $ {\rm{O}}(n^2) $ $ {\rm{O}}(s^2) $ $ - $ $ - $ 表中$ n $为训练数据集的样本数量, $ s $是诱导数据量, GP和稀疏GP的复杂度数据来自文献[20, 36]. 对RT和RF, $ F $表示特征数, $ D $表示树深度, $ T $表示森林中树木的数目, $ \tau=nFD $.
下载: 导出CSV
表 3 不同回归方法在测试数据集上的拟合误差对比表
Table 3 Fitting error comparison table of different regression methods on test datasets
项目 数据集 RT RF RTL RFL RMSE (‰) 训练集 1.60 1.52 0.16 0.15 测试集 1.57 1.48 0.15 0.14 ME (cm) 训练集 2.72 2.80 0.33 0.31 测试集 3.19 2.81 0.34 0.32
下载: 导出CSV
表 4 不同残差模型横向跟踪误差性能对比表
Table 4 Performance comparison table of lateral tracking error among different residual models
下载: 导出CSV
表 5 不同残差模型计算耗时对比表
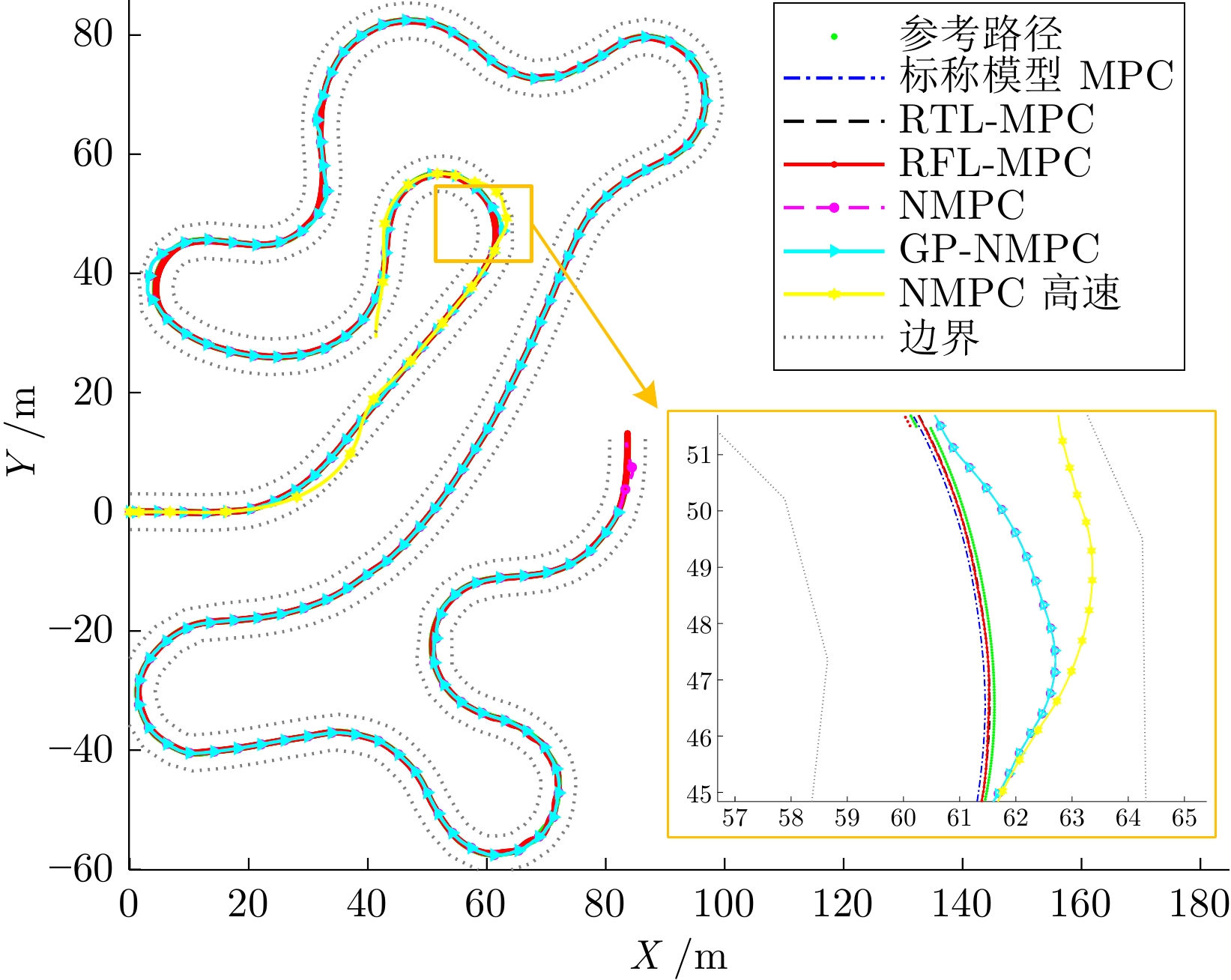
时间(s) MPC RTL-MPC RFL-MPC NMPC GP-NMPC 平均耗时 0.059 0.184 0.695 2.308 15.434 最大耗时 0.827 0.886 1.641 4.137 21.692 优化耗时 0.012 0.027 0.012 1.676 14.274
下载: 导出CSV
表 6 半拖挂卡车轨迹跟踪实验参数设置
Table 6 Parameter settings for trajectory tracking experiments of semi-trailer trucks
控制器参数 $ N_p $ $ N_c $ $ T_s $ $ q_c $ $ q_l $ $ q_{\phi} $ $ q_v $ $ R_u $ 仿真实验 60 60 0.02 10 10 1 4 1 实车实验 60 60 0.02 10 10 1 4 1
下载: 导出CSV
-
[1] Camacho E F, Alba C B. Model Predictive Control. Berlin: Springer Science & Business Media, 2013. [2] Hewing L, Wabersich K P, Menner M, Zeilinger M N. Learning-based model predictive control: Toward safe learning in control. Annual Review of Control, Robotics, and Autonomous Systems, 2020, 3(1): 269−296 doi: 10.1146/annurev-control-090419-075625 [3] Vicente B A H, James S S, Anderson S R. Linear system identification versus physical modeling of lateral-longitudinal vehicle dynamics. IEEE Transactions on Control Systems Technology, 2020, 29(3): 1380−1387 [4] Spielberg N A, Brown M, Kapania N R, Kegelman J C, Gerdes J C. Neural network vehicle models for high-performance automated driving. Science Robotics, 2019, 4(28): Article No. eaaw1975 doi: 10.1126/scirobotics.aaw1975 [5] Da Lio M, Bortoluzzi D, Rosati Papini G P. Modelling longitudinal vehicle dynamics with neural networks. Vehicle System Dynamics, 2020, 58(11): 1675−1693 doi: 10.1080/00423114.2019.1638947 [6] Xu J X, Luo Q, Xu K C, Xiao X Q, Yu S Y, Hu J T, et al. An automated learning-based procedure for large-scale vehicle dynamics modeling on Baidu Apollo platform. In: Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Macau: IEEE, 2019. 5049-5056 [7] McKinnon C D, Schoellig A P. Learning probabilistic models for safe predictive control in unknown environments. In: Proceedings of the 2019 European Control Conference (ECC). Naples: IEEE, 2019. 2506-2512 [8] Kabzan J, Hewing L, Liniger A, Zeilinger M N. Learning-based model predictive control for autonomous racing. IEEE Robotics and Automation Letters, 2019, 4(4): 3363−3370 doi: 10.1109/LRA.2019.2926677 [9] Hewing L, Liniger A, Zeilinger M N. Cautious NMPC with Gaussian process dynamics for autonomous miniature race cars. In: Proceedings of the 2018 European Control Conference (ECC). Limassol: IEEE, 2018. 1341-1348 [10] 韩陌, 何洪文, 石曼, 刘伟, 曹剑飞, 吴京达. 基于学习的无人驾驶车辆模型预测路径跟踪控制研究. 汽车工程, 2024, 46(7): 1197−1207Han Mo, He Hong-Wen, Shi Man, Liu Wei, Cao Jian-Fei, Wu Jing-Da. Research on learning-based model predictive path tracking control for autonomous vehicles. Automotive Engineering, 2024, 46(7): 1197−1207 [11] Ostafew C J, Schoellig A P, Barfoot T D. Learning-based nonlinear model predictive control to improve vision-based mobile robot path tracking. Journal of Field Robotics, 2016, 33(1): 133−152 doi: 10.1002/rob.21587 [12] Li F, Li H P, Wu C. Gaussian process based learning model predictive control with application to USV. IEEE Transactions on Industrial Electronics, 2024, 71(12): 16388−16397 doi: 10.1109/TIE.2024.3384617 [13] Panetsos F, Karras G C, Kyriakopoulos K J. GP-based NMPC for aerial transportation of suspended loads. IEEE Robotics and Automation Letters, 2024, 10(1): 524−531 [14] 方培俊, 蔡英凤, 陈龙, 廉玉波, 王海, 钟益林, 等. 基于车辆动力学混合模型的智能汽车轨迹跟踪控制方法. 汽车工程, 2022, 44(10): 1469−1483Fang Pei-Jun, Cai Ying-Feng, Chen Long, Lian Yu-Bo, Wang Hai, Zhong Yi-Lin, et al. Trajectory tracking control method based on vehicle dynamics hybrid model for intelligent vehicle. Automotive Engineering, 2022, 44(10): 1469−1483 [15] Albeaik S, Wu T, Vurimi G, Chou F C, Lu X Y, Bayen A M. Longitudinal deep truck: Deep longitudinal model with application to sim2real deep reinforcement learning for heavy-duty truck control in the field. Journal of Field Robotics, 2023, 40(2): 306−329 doi: 10.1002/rob.22131 [16] Rajamani R. Vehicle Dynamics and Control. New York: Springer Science & Business Media, 2011. [17] Quionero-Candela J, Rasmussen C E. A unifying view of sparse approximate Gaussian process regression. Journal of Machine Learning Research, 2005, 6: 1939−1959 [18] Lázaro-Gredilla M, Quionero-Candela J, Rasmussen C E, Figueiras-Vidal A R. Sparse spectrum Gaussian process regression. Journal of Machine Learning Research, 2010, 11(9): 1865−1881 [19] Gómez-Verdejo V, Parrado-Hernández E, Martínez-Ramón M. Adaptive sparse Gaussian process. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(11): 16383−16395 doi: 10.1109/TNNLS.2023.3294089 [20] Amer A, Mehndiratta M, Brodskiy Y, Kayacan E. Empowering autonomous underwater vehicles using learning-based model predictive control with dynamic forgetting Gaussian processes. IEEE Transactions on Control Systems Technology, 2025, 33(5): 1913−1920 doi: 10.1109/TCST.2025.3539218 [21] Chrosniak J, Ning J, Behl M. Deep dynamics: Vehicle dynamics modeling with a physics-constrained neural network for autonomous racing. IEEE Robotics and Automation Letters, 2024, 9(6): 5292−5297 doi: 10.1109/LRA.2024.3388847 [22] Miao J Y, Yan R J, Zhang B W, Wen T P, Li J Q, Fu Z, et al. Residual learning towards high-fidelity vehicle dynamics modeling with Transformer. IEEE Robotics and Automation Letters, 2025, 10(7): 7404−7411 doi: 10.1109/LRA.2025.3575637 [23] Smarra F, Jain A, de Rubeis T, Ambrosini D, D′Innocenzo A, Mangharam R. Data-driven model predictive control using random forests for building energy optimization and climate control. Applied Energy, 2018, 226: 1252−1272 doi: 10.1016/j.apenergy.2018.02.126 [24] Xu S, Peng H, Tang Y. Preview path tracking control with delay compensation for autonomous vehicles. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(5): 3130−3141 [25] Xing H, Ploeg J, Nijmeijer H. Padé approximation of delays in cooperative ACC based on string stability requirements. IEEE Transactions on Intelligent Vehicles, 2016, 1(3): 277−286 doi: 10.1109/TIV.2017.2662482 [26] Zhang L, Yin X, Wang Z, Sun F, Ding X. Hierarchical hybrid steering control for four-wheel-steering vehicles considering system delays. IEEE Transactions on Vehicular Technology, 2024, 73(2): 1234−1245 [27] Xu X, Liu Z Y, Wang F, Xie J, Su P W. Trajectory tracking control based on the dual-motor autonomous steering system with time-varying network-induced time delay. Control Engineering Practice, 2021, 116: Article No. 104915 doi: 10.1016/j.conengprac.2021.104915 [28] Gong Y, Zhu W X. Modeling and robust $ {H_ {\infty}} $ control synthesis of the CAV-HDV heterogeneous traffic system with different car-following modes. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(10): 12980−12998 doi: 10.1109/TITS.2024.3431591 [29] Fang R, Wang Z, Liang J, Yin G, Liu C, Liu H, et al. A vision-based robust ${H_ {\infty}}$ gain scheduling longitudinal and lateral following controller for autonomous vehicles on urban curved roads. IEEE Transactions on Intelligent Vehicles, 2024, 9(11): 7498−7513 doi: 10.1109/TIV.2024.3398739 [30] Zhang B, Wang C, Zhao W, Lian Y, Zhang H. The design and stable delay range analysis of TD-H2/ ${ H_ {\infty}} $ controller for SbW systems. IEEE Transactions on Transportation Electrification, 2024, 11(1): 404−15 [31] Vallinder G, Mårtensson J, Lima P F, Bhat S. Model predictive control for autonomous driving: Comparing kinematic and dynamic models of tractor-trailer systems. In: Proceedings of the 2024 IEEE 27th International Conference on Intelligent Transportation Systems (ITSC). Edmonton: IEEE, 2024. 3154−3159 [32] Liniger A, Domahidi A, Morari M. Optimization-based autonomous racing of 1: 43 scale RC car. Optimal Control Applications and Methods, 2015, 36(5): 628−647 doi: 10.1002/oca.2123 [33] Stellato B, Banjac G, Goulart P, Bemporad A, Boyd S. OSQP: An operator splitting solver for quadratic programs. Mathematical Programming Computation, 2020, 12(4): 637−672 doi: 10.1007/s12532-020-00179-2 [34] Ferreau H J, Kirches C, Potschka A, Bock H G, Diehl M. qpOASES: A parametric active-set algorithm for quadratic programming. Mathematical Programming Computation, 2014, 6(4): 327−363 doi: 10.1007/s12532-014-0071-1 [35] Frison G, Diehl M. HPIPM: A high-performance quadratic programming framework for model predictive control. IFAC-PapersOnLine, 2020, 53(2): 6563−6569 doi: 10.1016/j.ifacol.2020.12.073 [36] Liu H T, Ong Y S, Shen X B, Cai J F. When Gaussian process meets big data: A review of scalable GPs. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(11): 4405−4423 doi: 10.1109/TNNLS.2019.2957109 [37] Zhao K, Xue J R, Meng X N, Li G X, Wu M S. Learning residual model of model predictive control via random forests for autonomous driving. In: Proceedings of the 2024 IEEE 27th International Conference on Intelligent Transportation Systems (ITSC). Edmonton: IEEE, 2024. 755−761 -
下载:
计量
- 文章访问数: 9
- HTML全文浏览量: 3
- 被引次数: 0
